
Viés de Seleção
No post passado, falamos do crescimento exagerado do número de fatores reportados na literatura nos últimos 15 anos, chegando a 400 de acordo com Harvey e Liu (2019). Diante disso, uma propensão natural de qualquer pesquisador é testar o maior número de estratégias para que as melhores sejam selecionadas.
Neste post, nós discutimos como essa prática afeta a interpretação da métrica de desempenho mais utilizada no mercado, o índice de Sharpe. Para isso, nós utilizamos o caso extremo onde apenas uma estratégia é escolhida entre várias testadas. A metodologia utilizada é a proposta por Harvey e Liu (2015).
Parte V - Múltiplos testes e o índice de Sharpe
O primeiro passo nessa discussão é reconhecer que resultados obtidos através de simulações históricas (backtests) provavelmente exageram possíveis ganhos futuros. Uma das razões para isso é o fato de tais simulações envolverem algum grau de mineração dos dados (data mining).
Por exemplo, em uma situação onde inúmeras estratégias são testadas com o mesmo banco de dados, existe uma probabilidade de que alguma estratégia seja lucrativa por pura sorte. Dessa forma, é relativamente fácil para o pesquisador obter um backtest satisfatório após múltiplas simulações históricas.
A questão é se essa informação é revelada para o investidor. Quando o pesquisador apresenta tal backtest como se fosse o resultado de uma única tentativa, o desempenho dessa simulação se torna exagerado, em função do chamado viés de seleção (selection bias).
Gestores e investidores, cientes disso, costumam reduzir (descontar) resultados calculados com base em simulações históricas. Com relação ao índice de Sharpe, uma prática comum é reduzir esse índice em 50%.
Harvey e Liu (2015) argumentam, no entanto, que esse desconto não é apropriado. O desconto (haircut, como eles dizem) deve ser não linear. Índices de Sharpe baixos devem ser muito penalizados enquanto valores mais altos devem ter uma penalização menor.
A abordagem de Harvey e Liu
Harvey e Liu (2015) propõem uma metodologia de ajuste do índice de Sharpe em função do número de estratégias testadas (N) e do número de períodos (T) de uma determinada base de dados.1,2
O índice de Sharpe (IS) é a medida do retorno de um investimento ajustado pelo seu risco e pode ser calculado como a média do retorno em excesso (μ) por unidade de risco (σ, desvio padrão dos retornos em excesso): IS = μ / σ.
O teste proposto avalia se os retornos em excesso esperados são diferentes de zero, o que permite calcular a significância estatística da estratégia de investimento.3 De forma casual, podemos ilustrar essa metodologia da seguinte maneira.
Suponha que o índice de Sharpe de um determinado backtest seja igual a 1 (anualizado), obtido de uma amostra de 5 anos com retornos diários (T=1250). Primeiro, nós devemos calcular a probabilidade de que esse índice de Sharpe tenha acontecido por pura sorte, supondo que apenas uma estratégia tenha sido testada.4 No nosso exemplo, essa probabilidade é igual a 2,53%.
Digamos, no entanto, que tenhamos testado duas estratégias (N=2) e o valor reportado (IS=1) seja o da melhor estratégia. Utilizando a probabilidade para um único teste (2,53%), podemos calcular a probabilidade de que esse índice de Sharpe tenha acontecido por pura sorte.5 Nós obtemos o valor de 5,01%. Como esperado, essa probabilidade é maior, visto que tivemos duas chances para escolher a melhor estratégia.
Precisamos agora calcular o IS ajustado. Para isso, calculamos o índice de Sharpe que seria compatível com essa probabilidade de 5,01%, mas caso tivéssemos realizado apenas um teste.6 Obtemos o valor de 0,88, ou seja, um desconto (haircut) de 12,0%.
Aplicação
Vamos analisar como o IS ajustado varia em função do número de estratégias testadas (N), do IS reportado e do tamanho da amostra (T).
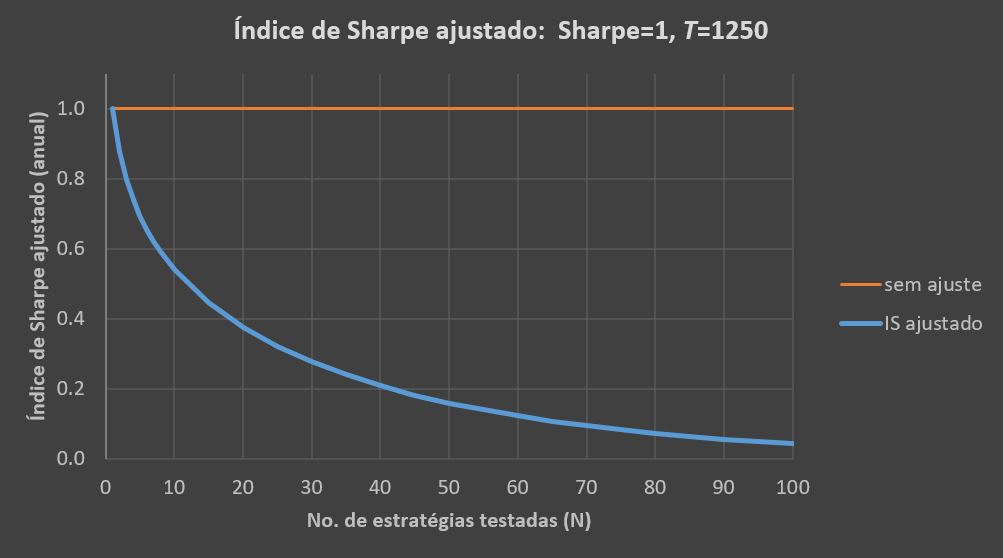
O gráfico a seguir ilustra a influência do número de estratégias testadas (N) para um backtest com índice de Sharpe igual a 1, obtido com uma amostra de 5 anos com retornos diários (T=1250). Como se vê, o IS ajustado decresce com o aumento do número de estratégias testadas. Em outras palavras, quanto mais estratégias forem testadas menos confiabilidade você deve ter no índice de Sharpe reportado.
Logo, para se avaliar o índice de Sharpe de algum backtest, é importante saber quantas estratégias foram testadas. Por exemplo, caso 20 estratégias tenham sido testadas, você deveria considerar que o índice de Sharpe é na realidade igual a 0,37, um desconto de 63%.
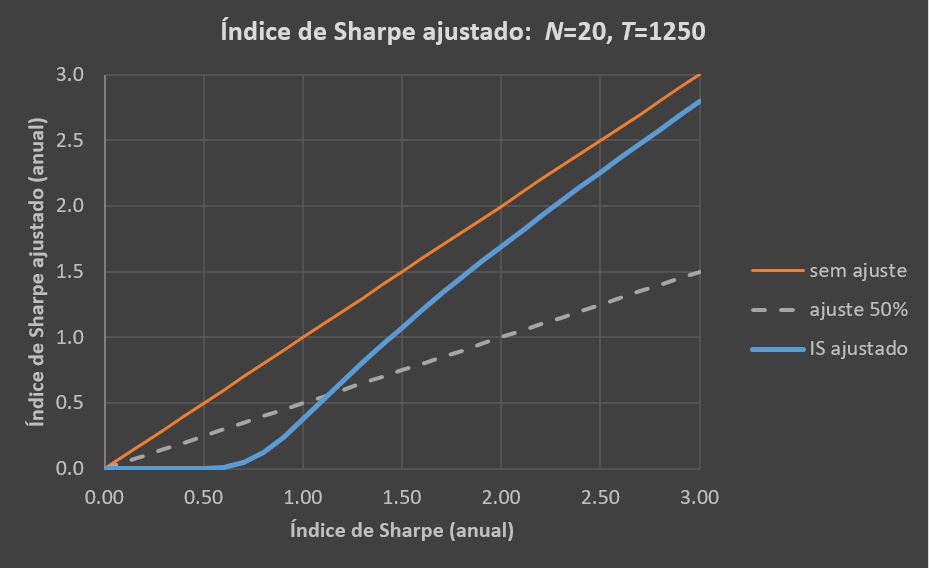
Agora, analisamos como o ajuste no IS é influenciado pelo valor do índice de Sharpe reportado no backtest. Nesse caso, foram testadas 20 estratégias para a mesma amostra com 1250 observações.
A reta amarela na diagonal do gráfico abaixo indica o IS caso não houvesse necessidade de ajuste. Como vimos no gráfico anterior, isso só acontece quando apenas uma estratégia é testada. A reta pontilhada indica a prática usual de redução do índice de Sharpe em 50%, enquanto a curva azul indica a correção proposta por Harvey e Liu.
Fica claro que o desconto deve ser feito de forma não linear: (i) Estratégias com IS muito baixos (abaixo de 0,7 nesse caso) devem receber um desconto de quase 100% e, por isso, não têm valor para o investidor; (ii) Até valores médios de IS (aproximadamente 1,15 no nosso exemplo), o desconto ainda deve ser maior do que a prática usual de 50%; e (iii) Estratégias com IS acima desse valor recebem um desconto menor, chegando a apenas 7% para um IS reportado igual a 3.
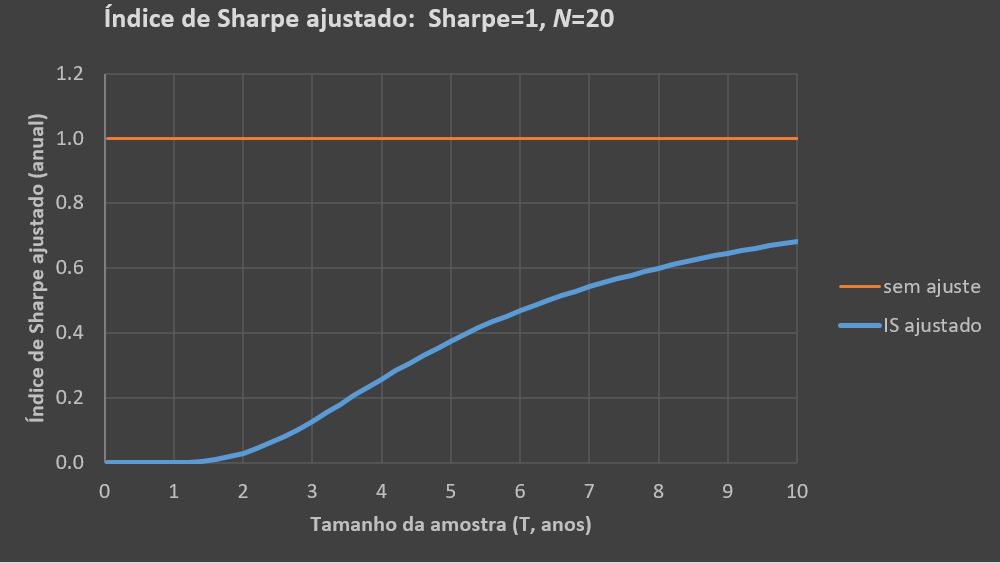
Finalmente, verificamos como o IS ajustado varia com o tamanho da amostra. Utilizamos um IS reportado igual a 1 sendo que 20 estratégias foram testadas. O gráfico mostra um aumento na confiabilidade do IS reportado quando amostras maiores são usadas. O IS ajustado varia de praticamente zero (100% de desconto) para uma amostra de um ano para 0,68 (desconto de 32%) com 10 anos de amostra.
Principais pontos
Nós mostramos que o desconto usual de 50% para o índice de Sharpe não é adequado e que esse desconto deve ser feito de forma não linear.
Além disso, nós vimos que a confiabilidade do índice de Sharpe reportado em um determinado backtest deve ser maior caso poucas estratégias tenham sido testadas, caso o tamanho da amostra seja grande e caso o valor do índice de Sharpe reportado seja alto.
No próximo artigo...
No post anterior, nós apresentamos uma classificação dos quase 400 fatores reportados na literatura. Isso naturalmente leva a uma testagem maior de possíveis estratégias de investimento. Neste post, nós indicamos como isso afeta a confiabilidade do índice de Sharpe apresentado em um backtest.
No próximo post, nós discutiremos como selecionar alguns entre tantos fatores de investimento. O objetivo é avaliar o conteúdo informacional adicional de cada fator em relação a um modelo já estabelecido. Para isso, nós apresentaremos o método tradicional e as chamadas spanning regressions.
Marco Lyrio
_________________________________
1 Nós utilizamos o caso mais simples. Os retornos são considerados independentes e identicamente distribuidos (i.i.d.) e seguem uma distribuição Gaussiana (Normal). As estratégias são consideradas independentes e toda a amostra disponível é utilizada (simulações dentro da amostra, in-sample).
2 Bailey e López de Prado (2014) propõem uma metodologia alternativa para a correção do índice de Sharpe em função do viés de seleção, overfitting e não normalidade dos retornos. A técnica proposta segue a linha da literatura de machine learning.
3 Os autores utilizam a relação entre a estatística t (razão t) e o índice de Sharpe. Como t = μ⁄(σ√ T ) , temos que t = IS √ T .
4 Esse é o p-valor com base em uma distribuição normal sob a hipótese nula de que o retorno em excesso médio da estratégia, e portanto seu índice de Sharpe, é igual a zero. O teste utiliza uma hipótese alternativa bilateral, assumindo que o investidor possa estar comprado ou vendido em determinada carteira. Para o cálculo do p-valor, precisamos da estatística t, nesse caso igual a t = (1⁄ √ 250 ) √ 1250 = 2,2360.
5 Com base no p-valor para um único teste (pS), o p-valor para o teste múltiplo (pM) é igual a:
pM = Pr(max{∣μi∣, i=1,2} > t)
pM = 1 − [ Pr(∣ μ1∣ ≤ t) Pr(∣ μ2∣ ≤ t) ]
pM = 1 − [ (1 − pS) (1 − pS) ]
pM = 1 − [ (1 − 0,0253) (1 − 0,0253) ]
pM = 0,0501.
6 A estatística t nesse caso é igual a 1,9595. Como t = IS √ T , temos que 1,9595 = (IS⁄ √ 250 ) √ 1250 , o que nos dá um IS anualizado de 0,8763.
_________________________________
REFERÊNCIAS
Bailey, D. H. e M. López de Prado (2014), "The deflated Sharpe ratio: Correcting for selection bias, backtest overfitting, and non-normality", Journal of Portfolio Management 40 (5), 94–107.
Harvey, C. R. e Y. Liu (2015), "Backtesting", Journal of Portfolio Management 42 (1), 13–28.
Harvey, C. R. e Y. Liu (2019), "A census of the factor zoo", SSRN Working Paper 3341728.